Algorithms
An algorithm is a step-by-step procedure for calculations. Algorithms are used for calculation, data processing, and automated reasoning.
More precisely, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Starting from an initial state and initial input (perhaps empty), the instructions describe a computation that, when executed, will proceed through a finite number of well-defined successive states, eventually producing "output" and terminating at a final ending state. The transition from one state to the next is not necessarily deterministic; some algorithms, known as randomized algorithms, incorporate random input.
Association rules Algorithms
Many algorithms for generating association rules were presented over time.
Some well known algorithms are Apriori, Eclat and FP-Growth, but they only do half the job, since they are algorithms for mining frequent itemsets. Another step needs to be done after to generate rules from frequent itemsets found in a database.
Apriori algorithm
Apriori is the best-known algorithm to mine association rules. It uses a breadth-first search strategy to count the support of itemsets and uses a candidate generation function which exploits the downward closure property of support.
Apriori is a classic algorithm for learning association rules. Apriori is designed to operate on databases containing transactions (for example, collections of items bought by customers, or details of a website frequentation). Other algorithms are designed for finding association rules in data having no transactions (Winepi and Minepi), or having no timestamps (DNA sequencing).
As is common in association rule mining, given a set of itemsets (for instance, sets of retail transactions, each listing individual items purchased), the algorithm attempts to find subsets which are common to at least a minimum number C of the itemsets. Apriori uses a "bottom up" approach, where frequent subsets are extended one item at a time (a step known as candidate generation), and groups of candidates are tested against the data. The algorithm terminates when no further successful extensions are found.
The purpose of the Apriori Algorithm is to find associations between different sets of data. It is sometimes referred to as "Market Basket Analysis". Each set of data has a number of items and is called a transaction. The output of Apriori is sets of rules that tell us how often items are contained in sets of data. Here is an example:
each line is a set of items
| alpha | beta | gamma |
| alpha | beta | theta |
| alpha | beta | epsilon |
| alpha | beta | theta |
- 100% of sets with alpha also contain beta
- 25% of sets with alpha, beta also have gamma
- 50% of sets with alpha, beta also have theta
Apriori uses breadth-first search and a Hash tree structure to count candidate item sets efficiently. It generates candidate item sets of length  from item sets of length
from item sets of length  . Then it prunes the candidates which have an infrequent sub pattern. According to the downward closure lemma, the candidate set contains all frequent
. Then it prunes the candidates which have an infrequent sub pattern. According to the downward closure lemma, the candidate set contains all frequent  -length item sets. After that, it scans the transaction database to determine frequent item sets among the candidates.
-length item sets. After that, it scans the transaction database to determine frequent item sets among the candidates.
Apriori, while historically significant, suffers from a number of inefficiencies or trade-offs, which have spawned other algorithms. Candidate generation generates large numbers of subsets (the algorithm attempts to load up the candidate set with as many as possible before each scan). Bottom-up subset exploration (essentially a breadth-first traversal of the subset lattice) finds any maximal subset S only after all  of its proper subsets.
of its proper subsets.
Algorithm Pseudocode
The pseudocode for the algorithm is given below for a transaction database  , and a support threshold of
, and a support threshold of  . Usual set theoretic notation is employed, though note that
. Usual set theoretic notation is employed, though note that  is a multiset.
is a multiset.  is the candidate set for level
is the candidate set for level  . Generate() algorithm is assumed to generate the candidate sets from the large itemsets of the preceding level, heeding the downward closure lemma.
. Generate() algorithm is assumed to generate the candidate sets from the large itemsets of the preceding level, heeding the downward closure lemma. ![count[c]](https://upload.wikimedia.org/math/a/2/8/a284e9fea0f8e3a2185d04dc91330e7c.png) accesses a field of the data structure that represents candidate set
accesses a field of the data structure that represents candidate set  , which is initially assumed to be zero. Many details are omitted below, usually the most important part of the implementation is the data structure used for storing the candidate sets, and counting their frequencies.
, which is initially assumed to be zero. Many details are omitted below, usually the most important part of the implementation is the data structure used for storing the candidate sets, and counting their frequencies.
Apriori
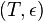

large 1-itemsets

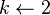
while

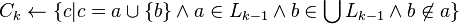
for transactions

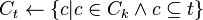
for candidates

![count[c] \gets count[c]+1](https://upload.wikimedia.org/math/0/6/8/06877396723fd139a75e2c0eb74db9f9.png)
![L_k \gets \{ c |c \in C_k \and ~ count[c] \geq \epsilon \}](https://upload.wikimedia.org/math/c/0/7/c074e501c8d3df66a7899d6bbb652e1e.png)
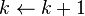
return

Example
A large supermarket tracks sales data by stock-keeping unit (SKU) for each item, and thus is able to know what items are typically purchased together. Apriori is a moderately efficient way to build a list of frequent purchased item pairs from this data. Let the database of transactions consist of the sets {1,2,3,4}, {1,2}, {2,3,4}, {2,3}, {1,2,4}, {3,4}, and {2,4}. Each number corresponds to a product such as "butter" or "bread". The first step of Apriori is to count up the frequencies, called the support, of each member item separately:
This table explains the working of apriori algorithm.
| Item | Support |
| 1 | 3/7 |
| 2 | 6/7 |
| 3 | 4/7 |
| 4 | 5/7 |
We can define a minimum support level to qualify as "frequent," which depends on the context. For this case, let min support = 3/7. Therefore, all are frequent. The next step is to generate a list of all pairs of the frequent items. Had any of the above items not been frequent, they wouldn't have been included as a possible member of possible pairs. In this way, Apriori prunes the tree of all possible sets. In next step we again select only these items (now pairs are items) which are frequent:
| Item | Support |
| {1,2} | 3/7 |
| {1,3} | 1/7 |
| {1,4} | 2/7 |
| {2,3} | 3/7 |
| {2,4} | 4/7 |
| {3,4} | 3/7 |
The pairs {1,2}, {2,3}, {2,4}, and {3,4} all meet or exceed the minimum support of 3/7. The pairs {1,3} and {1,4} do not. When we move onto generating the list of all triplets, we will not consider any triplets that contain {1,3} or {1,4}:
| Item | Support |
| {2,3,4} | 2/7 |
In the example, there are no frequent triplets -- {2,3,4} has support of 2/7, which is below our minimum, and we do not consider any other triplet because they all contain either {1,3} or {1,4}, which were discarded after we calculated frequent pairs in the second table.
Eclat algorithm
Eclat is a depth-first search algorithm using set intersection.
FP-growth algorithm
GUHA procedure ASSOC
GUHA is a general method for exploratory data analysis that has theoretical foundations in observational calculi.
The ASSOC procedure is a GUHA method which mines for generalized association rules using fast bitstrings operations. The association rules mined by this method are more general than those output by apriori, for example "items" can be connected both with conjunction and disjunctions and the relation between antecedent and consequent of the rule is not restricted to setting minimum support and confidence as in apriori: an arbitrary combination of supported interest measures can be used.
OPUS search
OPUS is an efficient algorithm for rule discovery that, in contrast to most alternatives, does not require either monotone or anti-monotone constraints such as minimum support. Initially used to find rules for a fixed consequent it has subsequently been extended to find rules with any item as a consequent. OPUS search is the core technology in the popular Magnum Opus association discovery system.

