Central Limit Theorem

 

Central Limit Theorem- What happens when repeated samples are taken from the same population? This idea is important when the central limit theorem for Six Sigma is used. If a coin is flipped ten times and one counts the number of heads that turns out, the laws of probability say that there is a 50-50 chance of getting heads on any single toss.

In practice, one may not get the expected five heads after flipping the coin ten times. Only three or heads turns up. After each experiment repetition (sample), the number of heads out of the ten flips is counted and the experiment is repeated 10, then 100, and finally 1,000 times.

This coin flip experiment is analogous to any situation where a sample of data from a population is taken. For example- a sample of measurements from a process and calculating the average. Two important facts arise from that one can generalize to any sampling situation:

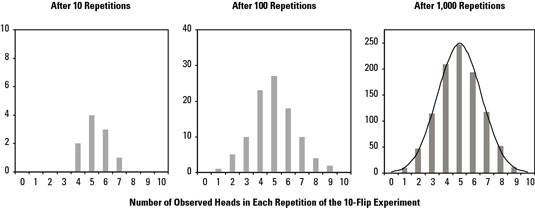
• Repetitions of the measurement event result in different outcomes. That is, the result is variable from sample to sample. In the coin-flipping experiment, not every repetition of the ten-flip series produced the expected five heads. The same is true if you repeatedly take a five-point average of the thickness of paper coming out of a paper mill.
• This resulting measurement, or sampling distribution, is normally distributed. The variation is also centered on the expected outcome. And the more repetitions that is made, the closer the sampling variation gets to a perfectly normal distribution.

Statisticians call repeated measurements of a characteristic or process samples. So the variation that occurs in repeated sampling events they call its sampling distribution.

The sample measurements themselves are not the only things that vary when dealing with repeated samples. Statisticians have refined and honed technical definitions of what is called the central limit theorem. Although each definition is equally mysterious, they say the same basic thing: When you calculate statistics on a sample, repeating those calculations on another sample from the same population will always give you a slightly different result.

Additionally, the collection of repeated calculated results will always have a distribution itself. This sampling variation follows a normal bell curve centered on the true variation of the underlying population. Further, the width of the sampling distribution depends on how many measurements you take in each sample. The larger your sample size, the narrower the sampling variation.

Go back to Tutorial                                                                                Go to Home Page