Golden mean rectangle

In geometry, a golden rectangle is a rectangle whose side lengths are in the golden ratio, , which is  (the Greek letter phi), where  is approximately 1.618.

In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. The figure on the right illustrates the geometric relationship. Expressed algebraically, for quantities a and b with a > b > 0,

(a+b)/a=a/b= where the Greek letter phi (φ) represents the golden ratio. Its value is: 1.6180339887.. The golden ratio is also called the golden section or golden mean. Other names include extreme and mean ratio, medial section, divine proportion, divine section, golden proportion, golden cut, and golden number.

Applications

Some twentieth-century artists and architects, including Le Corbusier and Dalí, have proportioned their works to approximate the golden ratio—especially in the form of the golden rectangle, in which the ratio of the longer side to the shorter is the golden ratio—believing this proportion to be aesthetically pleasing. Mathematicians since Euclid have studied the properties of the golden ratio, including its appearance in the dimensions of a regular pentagon and in a golden rectangle, which can be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has also been used to analyze the proportions of natural objects as well as man-made systems such as financial markets, in some cases based on dubious fits to data.

Aesthetics

De Divina Proportione, a three-volume work by Luca Pacioli, was published in 1509. Pacioli, a Franciscan friar, was known mostly as a mathematician, but he was also trained and keenly interested in art. De Divina Proportione explored the mathematics of the golden ratio.

Though it is often said that Pacioli advocated the golden ratio’s application to yield pleasing, harmonious proportions, Livio points out that the interpretation has been traced to an error in 1799, and that Pacioli actually advocated the Vitruvian system of rational proportions. Pacioli also saw Catholic religious significance in the ratio, which led to his work’s title. De Divina Proportione contains illustrations of regular solids by Leonardo da Vinci, Pacioli’s longtime friend and collaborator.

Architecture

The Parthenon’s façade as well as elements of its façade and elsewhere are said by some to be circumscribed by golden rectangles.^[24] Other scholars deny that the Greeks had any aesthetic association with golden ratio. Its occurrence in regular pentagons and decagons was duly observed, as well as in the dodecahedron (a regular polyhedron whose twelve faces are regular pentagons). It is indeed exemplary that the great Euclid, contrary to generations of mystics who followed, would soberly treat that number for what it is, without attaching to it other than its factual properties.

A 2004 geometrical analysis of earlier research into the Great Mosque of Kairouan reveals a consistent application of the golden ratio throughout the design, according to Boussora and Mazouz. They found ratios close to the golden ratio in the overall proportion of the plan and in the dimensioning of the prayer space, the court, and the minaret. The authors note, however, that the areas where ratios close to the golden ratio were found are not part of the original construction, and theorize that these elements were added in a reconstruction.

The Swiss architect Le Corbusier, famous for his contributions to the modern international style, centered his design philosophy on systems of harmony and proportion.

Le Corbusier’s faith in the mathematical order of the universe was closely bound to the golden ratio and the Fibonacci series, which he described as “rhythms apparent to the eye and clear in their relations with one another. And these rhythms are at the very root of human activities. They resound in man by an organic inevitability, the same fine inevitability which causes the tracing out of the Golden Section by children, old men, savages and the learned.”

Another Swiss architect, Mario Botta, bases many of his designs on geometric figures. Several private houses he designed in Switzerland are composed of squares and circles, cubes and cylinders. In a house he designed in Origlio, the golden ratio is the proportion between the central section and the side sections of the house.

Painting

The 16th-century philosopher Heinrich Agrippa drew a man over a pentagram inside a circle, implying a relationship to the golden ratio.

Leonardo da Vinci’s illustrations of polyhedral in De divina proportione (On the Divine Proportion) and his views that some bodily proportions exhibit the golden ratio have led some scholars to speculate that he incorporated the golden ratio in his paintings. But the suggestion that his Mona Lisa, for example, employs golden ratio proportions, is not supported by anything in Leonardo’s own writings. Similarly, although the Vitruvian Man is often shown in connection with the golden ratio, the proportions of the figure do not actually match it, and the text only mentions whole number ratios.

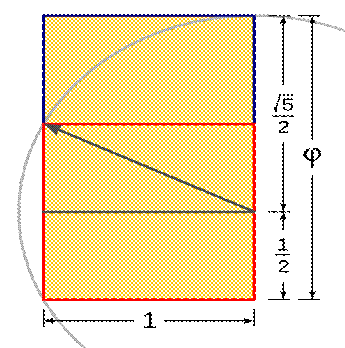
Construction of golden mean triangle

A golden rectangle can be constructed with only straightedge and compass by four simple steps

• Construct a simple square.
• Draw a line from the midpoint of one side of the square to an opposite corner.
• Use that line as the radius to draw an arc that defines the height of the rectangle.
• Complete the golden rectangle.