Three-dimensional space is a geometric 3-parameters model of the physical universe (without considering time) in which all known matter exists. These three dimensions can be labeled by a combination of three chosen from the terms length, width, height, depth, and breadth. Any three directions can be chosen, provided that they do not all lie in the same plane.
In physics and mathematics, a sequence of n numbers can be understood as a location in n-dimensional space. When n = 3, the set of all such locations is called 3-dimensional Euclidean space. It is commonly represented by the symbol . This space is only one example of a great variety of spaces in three dimensions called 3-manifolds.
In mathematics, analytic geometry (also called Cartesian geometry) describes any point in three-dimensional space by means of three coordinates. Three coordinate axes are given, usually each perpendicular to the other two at the origin, the point at which they cross. They are usually labeled x, y, and z. Relative to these axes, the position of any point in three-dimensional space is given by an ordered triple of real numbers, each number giving the distance of that point from the origin measured along the given axis, which is equal to the distance of that point from the plane determined by the other two axes.
Other popular methods of describing the location of a point in three-dimensional space include cylindrical coordinates and spherical coordinates, though there is an infinite number of possible methods. See Euclidean space.
Another mathematical way of viewing three-dimensional space is found in linear algebra, where the idea of independence is crucial. Space has three dimensions because the length of a box is independent of its width or breadth. In the technical language of linear algebra, space is three-dimensional because every point in space can be described by a linear combination of three independent vectors. In this view, space-time is four-dimensional because the location of a point in time is independent of its location in space.
Three-dimensional space has a number of properties that distinguish it from spaces of other dimension numbers. For example, at least three dimensions are required to tie a knotin a piece of string. Many of the laws of physics, such as the various inverse square laws, depend on dimension three.
The understanding of three-dimensional space in humans is thought to be learned during infancy using unconscious inference, and is closely related to hand-eye coordination. The visual ability to perceive the world in three dimensions is called depth perception. With the space , the topologists locally model all other 3-manifolds.
Co-ordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element on a manifold such as Euclidean space. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by a letter, as in “the x coordinate”. The coordinates are taken to be real numbers in elementary mathematics, but may be complex numbers or elements of a more abstract system such as a commutative ring. The use of a coordinate system allows problems in geometry to be translated into problems about numbers and vice versa; this is the basis of analytic geometry.
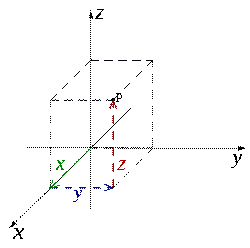
Cartesian co-ordinate system
The prototypical example of a coordinate system is the Cartesian coordinate system. In the plane, two perpendicular lines are chosen and the coordinates of a point are taken to be the signed distances to the lines.
In three dimensions, three perpendicular planes are chosen and the three coordinates of a point are the signed distances to each of the planes. This can be generalized to createn coordinates for any point in n-dimensional Euclidean space.
Depending on the direction and order of the coordinate axis the system may be a right-hand or a left-hand system.
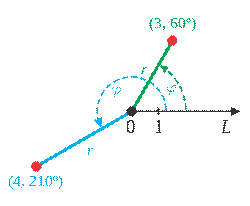
Polar co-ordinate system
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction.
The fixed point (analogous to the origin of a Cartesian system) is called the pole, and the ray from the pole in the fixed direction is the polar axis. The distance from the pole is called the radial coordinate or radius, and the angle is the angular coordinate, polar angle, or azimuth.
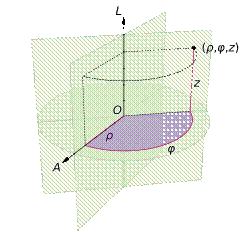
Cylindrical co-ordinate system
A cylindrical coordinate system is a three-dimensional coordinate system that specifies point positions by the distance from a chosen reference axis, the direction from the axis relative to a chosen reference direction, and the distance from a chosen reference plane perpendicular to the axis. The latter distance is given as a positive or negative number depending on which side of the reference plane faces the point.
The origin of the system is the point where all three coordinates can be given as zero. This is the intersection between the reference plane and the axis. The axis is variously called the cylindrical or longitudinal axis, to differentiate it from the polar axis, which is the ray that lies in the reference plane, starting at the origin and pointing in the reference direction.
The distance from the axis may be called the radial distance or radius, while the angular coordinate is sometimes referred to as the angular position or as the azimuth. The radius and the azimuth are together called the polar coordinates, as they correspond to a two-dimensional polar coordinate system in the plane through the point, parallel to the reference plane. The third coordinate may be called the height or altitude (if the reference plane is considered horizontal), longitudinal position, or axial position.
Cylindrical coordinates are useful in connection with objects and phenomena that have some rotational symmetry about the longitudinal axis, such as water flow in a straight pipe with round cross-section, heat distribution in a metal cylinder, electromagnetic fields produced by an electric current in a long, straight wire, and so on.
It is sometimes called “cylindrical polar coordinate” and “polar cylindrical coordinate”, and is sometimes used to specify the position of stars in a galaxy (“galactocentric cylindrical polar coordinate”).
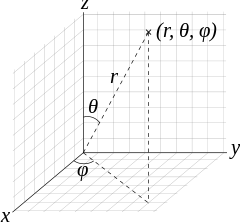
Spherical co-ordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its polar angle measured from a fixed zenith direction, and the azimuth angle of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction on that plane.
The radial distance is also called the radius or radial coordinate. The polar angle may be called co-altitude, zenith angle, normal angle, or inclination angle.
The use of symbols and the order of the coordinates differs between sources. In one system frequently encountered in physics (r, θ, φ) gives the radial distance, polar angle, and azimuthal angle, whereas in another system used in many mathematics books (r, θ, φ) gives the radial distance, azimuthal angle, and polar angle. In both systems ρ is often used instead of r. Other conventions are also used, so great care needs to be taken to check which one is being used.
A number of different spherical coordinate systems following other conventions are used outside mathematics. In a geographical coordinate system positions are measured in latitude, longitude and height or altitude. There are a number of different celestial coordinate systems based on different fundamental planes and with different terms for the various coordinates. The spherical coordinate systems used in mathematics normally use radians rather than degrees and measure the azimuthal angle counter-clockwise rather than clockwise. The inclination angle is often replaced by the elevation angle measured from the reference plane. Elevation angle of zero is at the horizon.
The concept of spherical coordinates can be extended to higher-dimensional spaces and are then referred to as hyper spherical coordinates.