Nonlinear regression is a form of regression analysis in which observational data are modeled by a function which is a nonlinear combination of the model parameters and depends on one or more independent variables. The data are fitted by a method of successive approximations.
While a linear equation has one basic form, nonlinear equations can take many different forms. The easiest way to determine whether an equation is nonlinear is to focus on the term “nonlinear” itself. Literally, it’s not linear. If the equation doesn’t meet the criteria above for a linear equation, it’s nonlinear.
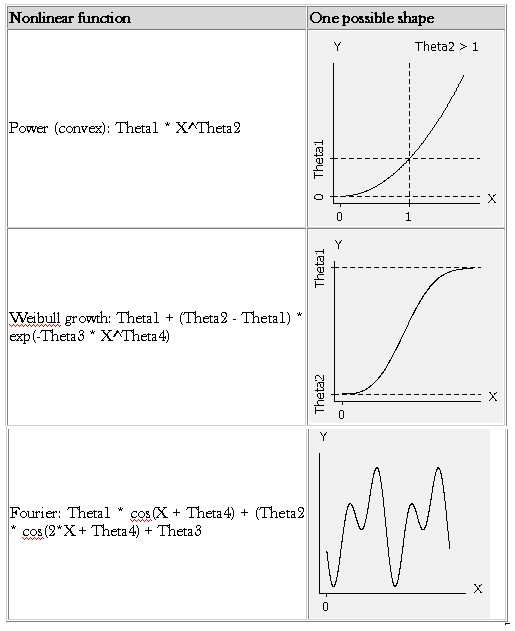
Unlike linear regression, these functions can have more than one parameter per predictor variable.
The data consist of error-free independent variables (explanatory variables), x, and their associated observed dependent variables (response variables), y. Each y is modeled as a random variable with a mean given by a nonlinear function f(x,β). Systematic error may be present but its treatment is outside the scope of regression analysis. If the independent variables are not error-free, this is an errors-in-variables model, also outside this scope.

Other examples of nonlinear functions include exponential functions, logarithmic functions, trigonometric functions, power functions, Gaussian function, and Lorenz curves. Some functions, such as the exponential or logarithmic functions, can be transformed so that they are linear. When so transformed, standard linear regression can be performed but must be applied with caution.
In general, there is no closed-form expression for the best-fitting parameters, as there is in linear regression. Usually numerical optimization algorithms are applied to determine the best-fitting parameters. Again in contrast to linear regression, there may be many local minima of the function to be optimized and even the global minimum may produce a biased estimate. In practice, estimated values of the parameters are used, in conjunction with the optimization algorithm, to attempt to find the global minimum of a sum of squares.

