Acoustics is the science of sound which deals with origin, propagation and auditory sensation of the sound. It also deals with design and construction of different building units to set optimum conditions for producing and listening speech, music, etc. Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics technology may be called an acoustical engineer. The application of acoustics is present in almost all aspects of modern society with the most obvious being the audio and noise control industries.
The knowledge and application of this science is vital for the construction and design of various structures and units such as theatres, discos, conference rooms, auditoriums, hospitals, etc.
The word “acoustic” is derived from the Greek word, meaning “of or for hearing, ready to hear” and that from, “heard, audible”, which in turn derives from the verb “I hear”.
The Latin synonym is “sonic”, after which the term sonics used to be a synonym for acoustics and later a branch of acoustics. Frequencies above and below the audible range are called “ultrasonic” and “infrasonic”, respectively.
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency, which emphasizes the contrast to spatial frequency and angular frequency. The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency. For example, if a newborn baby’s heart beats at a frequency of 120 times a minute, its period – the interval between beats – is half a second (60 seconds (i.e. a minute) divided by 120 beats).
In some fields, especially where frequency-domain analysis is used, the concept of frequency is applied only to sinusoidal phenomena, since in linear systems more complex periodic and non-periodic phenomena are most easily analyzed in terms of sums of sinusoids of different frequencies.
For cyclical processes, such as rotation, oscillations, or waves, frequency is defined as a number of cycles per unit time. In physics and engineering disciplines, such as optics, acoustics, and radio, frequency is usually denoted by a Latin letter f or by the Greek letter ν (nu). Note, the related concept, angular frequency, is usually denoted by the Greek letter ω (omega), which uses the SI unit radians per second (rad/s).
For counts per unit of time, the SI unit for frequency is hertz (Hz), named after the German physicist Heinrich Hertz; 1 Hz means that an event repeats once per second. A previous name for this unit was cycles per second (cps).
A traditional unit of measure used with rotating mechanical devices is revolutions per minute, abbreviated r/min or rpm. 60 r/min equals one hertz. The period, usually denoted by T, is the duration of one cycle, and is the reciprocal of the frequency f:
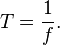
The SI unit for period is the second. Other than waves frequency related to occurrence of something can be denoted by
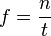
Where n is no. of times an event occurred and is the time
The frequency range of a system is the range over which it is considered to provide a useful level of signal with acceptable distortion characteristics. A listing of the upper and lower limits of frequency limits for a system is not useful without a criterion for what the range represents.
Many systems are characterized by the range of frequencies to which they respond. Musical instruments produce different ranges of notes within the hearing range. The electromagnetic spectrum can be divided into many different ranges such as visible light, infrared or ultraviolet radiation, radio waves, X-rays and so on, and each of these ranges can in turn be divided into smaller ranges. A radio communications signal must occupy a range of frequencies carrying most of its energy, called its bandwidth. Allocation of radio frequency ranges to different uses is a major function of radio spectrum allocation.
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave’s shape repeats. It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a characteristic of both traveling waves and standing waves, as well as other spatial wave patterns. Wavelength is commonly designated by the Greek letter lambda (λ). The concept can also be applied to periodic waves of non-sinusoidal shape. The term wavelength is also sometimes applied to modulated waves, and to the sinusoidal envelopes of modulated waves or waves formed by interference of several sinusoids. The SI unit of wavelength is the meter.
Assuming a sinusoidal wave moving at a fixed wave speed, wavelength is inversely proportional to frequency of the wave: waves with higher frequencies have shorter wavelengths, and lower frequencies have longer wavelengths.
Examples of wave-like phenomena are sound waves, light, and water waves. A sound wave is a variation in air pressure, while in light and other electromagnetic radiation the strength of the electric and the magnetic field vary. Water waves are variations in the height of a body of water. In a crystal lattice vibration, atomic positions vary.
Wavelength is a measure of the distance between repetitions of a shape feature such as peaks, valleys, or zero-crossings, not a measure of how far any given particle moves. For example, in sinusoidal waves over deep water a particle near the water’s surface moves in a circle of the same diameter as the wave height, unrelated to wavelength.
Sub-wavelength – The term sub-wavelength is used to describe an object having one or more dimensions smaller than the length of the wave with which the object interacts. For example, the term sub-wavelength-diameter optical fiber means an optical fiber whose diameter is less than the wavelength of light propagating through it.
A sub-wavelength particle is a particle smaller than the wavelength of light with which it interacts (see Rayleigh scattering). Sub-wavelength apertures are holes smaller than the wavelength of light propagating through them. Such structures have applications in extraordinary optical transmission, and zero-mode waveguides, among other areas of photonics.
Sub-wavelength may also refer to a phenomenon involving sub-wavelength objects; for example, sub-wavelength imaging.
Angular wavelength – A quantity related to the wavelength is the angular wavelength (also known as reduced wavelength), usually symbolized by ƛ (lambda-bar). It is equal to the “regular” wavelength “reduced” by a factor of 2π (ƛ = λ/2π). It is usually encountered in quantum mechanics, where it is used in combination with the reduced Planck constant (symbol ħ, h-bar) and the angular frequency (symbol ω) or angular wave number (symbol k).
Wave Number
In the physical sciences, the wave number (also wave number) is the spatial frequency of a wave, either in cycles per unit distance or radians per unit distance. It can be envisaged as the number of waves that exist over a specified distance (analogous to frequency being the number of cycles or radians per unit time).
Because of the use of this term in applied physics, including spectroscopy, often the reference distance should be assumed to be cm. For example, a particle’s energy may be given as a wave number in cm−1, which strictly speaking is not a unit of energy. However if one assumes this corresponds to electromagnetic radiation, then it can be directly converted to any unit of energy, e.g. 1 cm−1 implies 1.23984×10−4 eV and 8065.54 cm−1 implies 1 eV.
In multidimensional systems, the wave number is also the magnitude of the wave vector.
Amplitude
The amplitude of a periodic variable is a measure of its change over a single period (such as time or spatial period). There are various definitions of amplitude, which are all functions of the magnitude of the difference between the variable’s extreme values. In older texts the phase is sometimes called the amplitude.
Peak to Peak amplitude – Peak-to-peak amplitude is the change between peak (highest amplitude value) and trough (lowest amplitude value, which can be negative). With appropriate circuitry, peak-to-peak amplitudes of electric oscillations can be measured by meters or by viewing the waveform on an oscilloscope. Peak-to-peak is a straightforward measurement on an oscilloscope, the peaks of the waveform being easily identified and measured against the graticule. This remains a common way of specifying amplitude, but sometimes other measures of amplitude are more appropriate.
Peak amplitude – In audio system measurements, telecommunications and other areas where the measured is a signal that swings above and below a zero value but is not sinusoidal, peak amplitude is often used. This is the maximum absolute value of the signal.
Semi-amplitude – Semi-amplitude means half the peak-to-peak amplitude. It is the most widely used measure of orbital amplitude in astronomy and the measurement of small semi-amplitudes of nearby stars is important in the search for exo planets. Some scientists use “amplitude” or “peak amplitude” to mean semi-amplitude, that is, half the peak-to-peak amplitude.
Root mean square amplitude – Root mean square (RMS) amplitude is used especially in electrical engineering: the RMS is defined as the square root of the mean over time of the square of the vertical distance of the graph from the rest state.
For complex waveforms, especially non-repeating signals like noise, the RMS amplitude is usually used because it is both unambiguous and has physical significance. For example, the average power transmitted by an acoustic or electromagnetic wave or by an electrical signal is proportional to the square of the RMS amplitude (and not, in general, to the square of the peak amplitude).
For alternating current electric power, the universal practice is to specify RMS values of a sinusoidal waveform. One property of root mean square voltages and currents is that they produce the same heating effect as DC in a given resistance.
The peak-to-peak voltage of a sine wave is about 2.8 times the RMS value. The peak-to-peak value is used, for example, when choosing rectifiers for power supplies, or when estimating the maximum voltage insulation must withstand. Some common voltmeters are calibrated for RMS amplitude, but respond to the average value of a rectified waveform. Many digital voltmeters and all moving coil meters are in this category. The RMS calibration is only correct for a sine wave input since the ratio between peak, average and RMS values is dependent on waveform. If the wave shape being measured is greatly different from a sine wave, the relationship between RMS and average value changes. True RMS-responding meters were used in radio frequency measurements, where instruments measured the heating effect in a resistor to measure current. The advent of microprocessor controlled meters capable of calculating RMS by sampling the waveform has made true RMS measurement commonplace.
Sound Pressure
Sound pressure or acoustic pressure is the local pressure deviation from the ambient (average, or equilibrium) atmospheric pressure, caused by a sound wave. In air, sound pressure can be measured using a microphone, and in water with a hydrophone. The SI unit for sound pressure p is the pascal (symbol: Pa).
Sound pressure level (SPL) or sound level is a logarithmic measure of the effective sound pressure of a sound relative to a reference value. It is measured in decibels (dB) above a standard reference level. The standard reference sound pressure in air or other gases is 20µPa, which is usually considered the threshold of human hearing (at 1 kHz).
Sound Intensity
Sound intensity or acoustic intensity (I) is defined as the sound power Pac per unit area A. The usual context is the noise measurement of sound intensity in the air at a listener’s location as a sound energy quantity.
Sound intensity is not the same physical quantity as sound pressure. Hearing is directly sensitive to sound pressure which is related to sound intensity. In consumer audio electronics, the level differences are called “intensity” differences, but sound intensity is a specifically defined quantity and cannot be sensed by a simple microphone. The intensity is the product of the sound pressure and the particle velocity
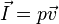
Speed of Sound
The speed of sound is the distance travelled per unit of time by a sound wave propagating through an elastic medium. In dry air at 20 °C (68 °F), the speed of sound is 343 metres per second (1,125 ft/s). This is 1,234 kilometers per hour (666 kn; 767 mph), or about a kilometer in three seconds or a mile in five seconds.
In fluid dynamics, the speed of sound in a fluid medium (gas or liquid) is used as a relative measure of speed itself. The speed of an object divided by the speed of sound in the fluid is called the Mach number. Objects moving at speeds greater than Mach1 are traveling at supersonic speeds.
The speed of sound in an ideal gas is independent of frequency, but does vary slightly with frequency in a real gas. It is proportional to the square root of the absolute temperature, but is independent of pressure or density for a given ideal gas. Sound speed in air varies slightly with pressure only because air is not quite an ideal gas. Although (in the case of gases only) the speed of sound is expressed in terms of a ratio of both density and pressure, these quantities cancel in ideal gases at any given temperature, composition, and heat capacity. This leads to a velocity formula for ideal gases which includes only the latter independent variables.
In common everyday speech, speed of sound refers to the speed of sound waves in air. However, the speed of sound varies from substance to substance. Sound travels faster in liquids and non-porous solids than it does in air. It travels about 4.3 times as fast in water (1,484 m/s), and nearly 15 times as fast in iron (5,120 m/s), as in air at 20 degrees Celsius. Sound waves in solids are composed of compression waves (just as in gases and liquids), but there is also a different type of sound wave called a shear wave, which occurs only in solids. These different types of waves in solids usually travel at different speeds, as exhibited in seismology. The speed of a compression sound wave in solids is determined by the medium’s compressibility, shear modulus and density. The speed of shear waves is determined only by the solid material’s shear modulus and density.

