Key exchange also called as key establishment, is method to exchange cryptographic keys between users, using a cryptographic algorithm. If the cipher is a symmetric key cipher, both will need a copy of the same key. If an asymmetric key cipher with the public/private key property, both will need the other’s public key.
Prior to any secured communication, users must set up the details of the cryptography. In some instances this may require exchanging identical keys (in the case of a symmetric key system). In others it may require possessing the other party’s public key. While public keys can be openly exchanged (their corresponding private key is kept secret), symmetric keys must be exchanged over a secure communication channel.
Formerly, exchange of such a key was extremely troublesome, and was greatly eased by access to secure channels such as a diplomatic bag. Clear text exchange of symmetric keys would enable any interceptor to immediately learn the key, and any encrypted data.
The advance of public key cryptography in the 1970s has made the exchange of keys less troublesome. Since the Diffie-Hellman key exchange protocol was published in 1975, it has become possible to exchange a key over an insecure communications channel, which has substantially reduced the risk of key disclosure during distribution. It is possible, using something akin to a book code, to include key indicators as clear text attached to an encrypted message. The encryption technique used by Richard Sorge’s code clerk was of this type, referring to a page in a statistical manual, though it was in fact a code. The German Army Enigma symmetric encryption key was a mixed type early in its use; the key was a combination of secretly distributed key schedules and a user chosen session key component for each message.
In more modern systems, such as OpenPGP compatible systems, a session key for a symmetric key algorithm is distributed encrypted by an asymmetric key algorithm. This approach avoids even the necessity for using a key exchange protocol like Diffie-Hellman key exchange.
Another method of key exchange involves encapsulating one key within another. Typically a master key is generated and exchanged using some secure method. This method is usually cumbersome or expensive (breaking a master key into multiple parts and sending each with a trusted courier for example) and not suitable for use on a larger scale. Once the master key has been securely exchanged, it can then be used to securely exchange subsequent keys with ease. This technique is usually termed Key Wrap. A common technique uses Block ciphers and cryptographic hash functions.
A related method is to exchange a master key (sometimes termed a root key) and derive subsidiary keys as needed from that key and some other data (often referred to as diversification data). The most common use for this method is probably in SmartCard based cryptosystems, such as those found in banking cards. The bank or credit network embeds their secret key into the card’s secure key storage during card production at a secured production facility. Then at the Point of sale the card and card reader are both able to derive a common set of session keys based on the shared secret key and card-specific data (such as the card serial number). This method can also be used when keys must be related to each other (i.e., departmental keys are tied to divisional keys, and individual keys tied to departmental keys). However, tying keys to each other in this way increases the damage which may result from a security breach as attackers will learn something about more than one key. This reduces entropy, with regard to an attacker, for each key involved.
Two of the most common key exchange algorithms are
- Diffie-Hellman Key Agreement algorithm
- RSA key exchange process
Both methods provide for highly secure key exchange between communicating parties. An intruder who intercepts network communications cannot easily guess or decode the secret key that is required to decrypt communications. The exact mechanisms and algorithms that are used for key exchange varies for each security technology. In general, the Diffie-Hellman Key Agreement algorithm provides better performance than the RSA key exchange algorithm.
Diffie-Hellman Key Agreement – Public key cryptography was first publicly proposed in 1975 by Stanford University researchers Whitfield Diffie and Martin Hellman to provide a secure solution for confidentially exchanging information online. Figure 14.5 shows the basic Diffie-Hellman Key Agreement process.
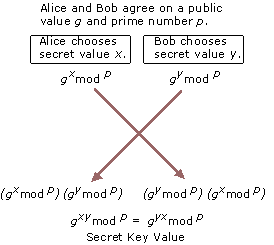
Diffie-Hellman key agreement is not based on encryption and decryption, but instead relies on mathematical functions that enable two parties to generate a shared secret key for exchanging information confidentially online. Essentially, each party agrees on a public value g and a large prime number p. Next, one party chooses a secret value x and the other party chooses a secret value y. Both parties use their secret values to derive public values, g x mod p and g y mod p, and they exchange the public values. Each party then uses the other party’s public value to calculate the shared secret key that is used by both parties for confidential communications. A third party cannot derive the shared secret key because they do not know either of the secret values, x or y.
For example, Alice chooses secret value x and sends the public value g x mod p to Bob. Bob chooses secret value y and sends the public value g y mod p to Alice. Alice uses the value g xy mod p as her secret key for confidential communications with Bob. Bob uses the value g yx mod p as his secret key. Because g xy mod p equals g yx mod p , Alice and Bob can use their secret keys with a symmetric key algorithm to conduct confidential online communications. The use of the modulo function ensures that both parties can calculate the same secret key value, but an eavesdropper cannot. An eavesdropper can intercept the values of g and p , but because of the extremely difficult mathematical problem created by the use of a large prime number in mod p, the eavesdropper cannot feasibly calculate either secret value x or secret value y . The secret key is known only to each party and is never visible on the network.
Diffie-Hellman key exchange is widely used with varying technical details by Internet security technologies, such as IPSec and TLS, to provide secret key exchange for confidential online communications. For technical discussions about Diffie-Hellman key agreement and how it is implemented in security technologies, see the cryptography literature that is referenced under
RSA Key Exchange – The Rivest-Shamir-Adleman (RSA) algorithms available from RSA Data Security, Inc., are the most widely used public key cryptography algorithms. For RSA key exchange, secret keys are exchanged securely online by encrypting the secret key with the intended recipient’s public key. Only the intended recipient can decrypt the secret key because it requires the use of the recipient’s private key. Therefore, a third party who intercepts the encrypted, shared secret key cannot decrypt and use it. The below figure illustrates the basic RSA key exchange process.

The RSA key exchange process is used by some security technologies to protect encryption keys. For example, EFS uses the RSA key exchange process to protect the bulk encryption keys that are used to encrypt and decrypt files.

