Statistical inference is the process of drawing conclusions about populations or scientific truths from data. There are many modes of performing inference including statistical modeling, data oriented strategies and explicit use of designs and randomization in analyses. Furthermore, there are broad theories (frequentists, Bayesian, likelihood, design based, …) and numerous complexities (missing data, observed and unobserved confounding, biases) for performing inference.
Statistical inference makes propositions about a population, using data drawn from the population with some form of sampling. Given a hypothesis about a population, for which we wish to draw inferences, statistical inference consists of (firstly) selecting a statistical model of the process that generates the data and (secondly) deducing propositions from the model.
The conclusion of a statistical inference is a statistical proposition. Some common forms of statistical proposition are the following:
- a point estimate, i.e. a particular value that best approximates some parameter of interest;
- an interval estimate, e.g. a confidence interval (or set estimate), i.e. an interval constructed using a dataset drawn from a population so that, under repeated sampling of such datasets, such intervals would contain the true parameter value with the probability at the stated confidence level;
- a credible interval, i.e. a set of values containing, for example, 95% of posterior belief;
- rejection of a hypothesis;
- clustering or classification of data points into groups.
Hypothesis testing, is a decision-making process for evaluating claims about a population. In hypothesis testing, the researcher must define the population under study, state the particular hypotheses that will be investigated, give the significance level, select a sample from the population, collect the data, perform the calculations required for the statistical test, and reach a conclusion
Hypotheses concerning parameters such as means and proportions can be investigated. There are two specific statistical tests used for hypotheses concerning means: the z test and the t test.
The three methods used to test hypotheses are
- The traditional method
- The P-value method
- The confidence interval method
Traditional Method of Hypothesis Testing
Every hypothesis-testing situation begins with the statement of a hypothesis. A statistical hypothesis is a conjecture about a population parameter. This conjecture may or may not be true. There are two types of statistical hypotheses for each situation: the null hypothesis and the alternative hypothesis.
The null hypothesis, symbolized by H0, is a statistical hypothesis that states that there is no difference between a parameter and a specific value, or that there is no difference between two parameters. The alternative hypothesis, symbolized by H1, is a statistical hypothesis that states the existence of a difference between a parameter and a specific value, or states that there is a difference between two parameters.
The null hypothesis is usually the accepted theory that the analyst is trying to disprove. In the previous examples the null hypotheses are
- The new packaging design is no better than the current design.
- The new drug has a cure rate no higher than other drugs on the market.
- Smokers are no more susceptible to heart disease than nonsmokers.
The burden of proof is traditionally on the alternative hypothesis. It is up to the analyst to provide enough evidence in support of the alternative; otherwise, the null hypothesis will continue to be accepted.
Example
Medical researcher is interested in finding out whether a new medication will have any undesirable side effects. The researcher is particularly concerned with the pulse rate of the patients who take the medication. Will the pulse rate increase, decrease, or remain unchanged after a patient takes the medication?
Since the researcher knows that the mean pulse rate for the population under study is 82 beats per minute, the hypotheses for this situation are
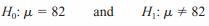
The null hypothesis specifies that the mean will remain unchanged, and the alternative hypothesis states that it will be different. This test is called a two-tailed test, since the possible side effects of the medicine could be to raise or lower the pulse rate.
Example
A chemist invents an additive to increase the life of an automobile battery. If the mean lifetime of the automobile battery without the additive is 36 months, then her hypotheses are
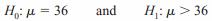
In this situation, the chemist is interested only in increasing the lifetime of the batteries, so her alternative hypothesis is that the mean is greater than 36 months. The null hypothesis is that the mean is equal to 36 months. This test is called right-tailed, since the interest is in an increase only.
Hypothesis Data
Hypothesis tests can be used to evaluate many different parameters of a population. Each test is designed to evaluate a parameter associated with a certain type of data. Knowing the difference between the types of data, and which parameters are associated with each data type, can help you choose the most appropriate test.
- Continuous Data – You will have continuous data when you evaluate the mean, median, standard deviation, or variance. When you measure a characteristic of a part or process, such as length, weight, or temperature, you usually obtain continuous data. Continuous data often includes fractional (or decimal) values. For example, a quality engineer wants to determine whether the mean weight differs from the value stated on the package label (500 g). The engineer samples cereal boxes and records their weights.
- Binomial Data – You will have binomial data when you evaluate a proportion or a percentage. When you classify an item, event, or person into one of two categories you obtain binomial data. The two categories should be mutually exclusive, such as yes/no, pass/fail, or defective/non-defective. For example, engineers examine a sample of bolts for severe cracks that make the bolts unusable. They record the number of bolts that are inspected and the number of bolts that are rejected. The engineers want to determine whether the percentage of defective bolts is less than 0.2%.
- Poisson Data – You will have Poisson data when you evaluate a rate of occurrence. When you count the presence of a characteristic, result, or activity over a certain amount of time, area, or other length of observation, you obtain Poisson data. Poisson data are evaluated in counts per unit, with the units the same size. For example, inspectors at a bus company count the number of bus breakdowns each day for 30 days. The company wants to determine the daily rate of bus breakdowns.
One-Tailed and Two-Tailed Tests
The form of the alternative hypothesis can be either one-tailed or two-tailed, depending on what the analyst is trying to prove. The only sample results that will lead to rejection of the null hypothesis are those in a particular direction, namely, those where the sample mean rating is positive. In contrast, a two-tailed test is one where results in either of two directions can lead to rejection of the null hypothesis. In this case either a large positive sample mean or a large negative sample mean will lead to rejection of the null hypothesis—and presumably to discontinuing one of the production methods.
Directional and non-directional hypotheses
A non-directional alternative hypothesis states that the null hypothesis is wrong. A non-directional alternative hypothesis does not predict whether the parameter of interest is larger or smaller than the reference value specified in the null hypothesis.
A directional alternative hypothesis states that the null hypothesis is wrong, and also specifies whether the true value of the parameter is greater than or less than the reference value specified in null hypothesis.
The advantage of using a directional hypothesis is increased power to detect the specific effect you are interested in. The disadvantage is that there is no power to detect an effect in the opposite direction.
Example
- Non-directional – A researcher has results for a sample of students who took a national exam at a high school. The researcher wants to know if the scores at that school differ from the national average of 850. A non-directional alternative hypothesis is appropriate because the researcher is interested in determining whether the scores are either less than or greater than the national average. (H0: μ = 850 vs. H1: μ≠ 850)
- Directional – A researcher has exam results for a sample of students who took a training course for a national exam. The researcher wants to know if trained students score above the national average of 850. A directional alternative hypothesis can be used because the researcher is specifically hypothesizing that scores for trained students are greater than the national average. (H0: μ = 850 vs. H1: μ > 850)
Type I and II errors
When you do a hypothesis test, two types of errors are possible: type I and type II. The risks of these two errors are inversely related and determined by the level of significance and the power for the test. Therefore, you should determine which error has more severe consequences for your situation before you define their risks. No hypothesis test is 100% certain. Because the test is based on probabilities, there is always a chance of drawing an incorrect conclusion.
Type I error – When the null hypothesis is true and you reject it, you make a type I error. The probability of making a type I error is α, which is the level of significance you set for your hypothesis test. An α of 0.05 indicates that you are willing to accept a 5% chance that you are wrong when you reject the null hypothesis. To lower this risk, you must use a lower value for α. However, using a lower value for alpha means that you will be less likely to detect a true difference if one really exists.
Type II error – When the null hypothesis is false and you fail to reject it, you make a type II error. The probability of making a type II error is β, which depends on the power of the test. You can decrease your risk of committing a type II error by ensuring your test has enough power. You can do this by ensuring your sample size is large enough to detect a practical difference when one truly exists.
The probability of rejecting the null hypothesis when it is false is equal to 1–β. This value is the power of the test.
| Null Hypothesis | ||
| Decision | True | False |
| Fail to reject | Correct Decision (probability = 1 – α) | Type II Error – fail to reject the null when it is false (probability = β) |
| Reject | Type I Error – rejecting the null when it is true (probability = α) | Correct Decision (probability = 1 – β) |
Example
A medical researcher wants to compare the effectiveness of two medications. The null and alternative hypotheses are
- Null hypothesis (H0): μ1= μ The two medications are equally effective.
- Alternative hypothesis (H1): μ1≠ μ The two medications are not equally effective.
A type I error occurs if the researcher rejects the null hypothesis and concludes that the two medications are different when, in fact, they are not. If the medications have the same effectiveness, the researcher may not consider this error too severe because the patients still benefit from the same level of effectiveness regardless of which medicine they take. However, if a type II error occurs, the researcher fails to reject the null hypothesis when it should be rejected. That is, the researcher concludes that the medications are the same when, in fact, they are different. This error is potentially life-threatening if the less-effective medication is sold to the public instead of the more effective one.
As you conduct your hypothesis tests, consider the risks of making type I and type II errors. If the consequences of making one type of error are more severe or costly than making the other type of error, then choose a level of significance and a power for the test that will reflect the relative severity of those consequences.

